Bayes For Everyone

A guest post by Brandon Hendrickson

[Editor’s note: I accept guest posts from certain people, especially past Book Review Contest winners. Brandon Hendrickson, whose review of The Educated Mind won the 2023 contest, has taken me up on this and submitted this essay. He writes at The Lost Tools of Learning and will be at LessOnline this weekend, where he and Jack Despain Zhou aka TracingWoodgrains will be doing a live conversation about education.]

I began my book review of a couple years back with a rather simple question:

Could a new kind of school make the world rational?

What followed, however, was a sprawling distillation of one scholar’s answer that I believe still qualifies as “the longest thing anyone has submitted for an ACX contest”. Since then I’ve been diving into particulars, exploring how we use the insights I learned while writing it to start re-enchanting all the academic subjects from kindergarten to high school. But in the fun of all that, I fear I’ve lost touch with that original question. How, even in theory, could a method of education help all students become rational?

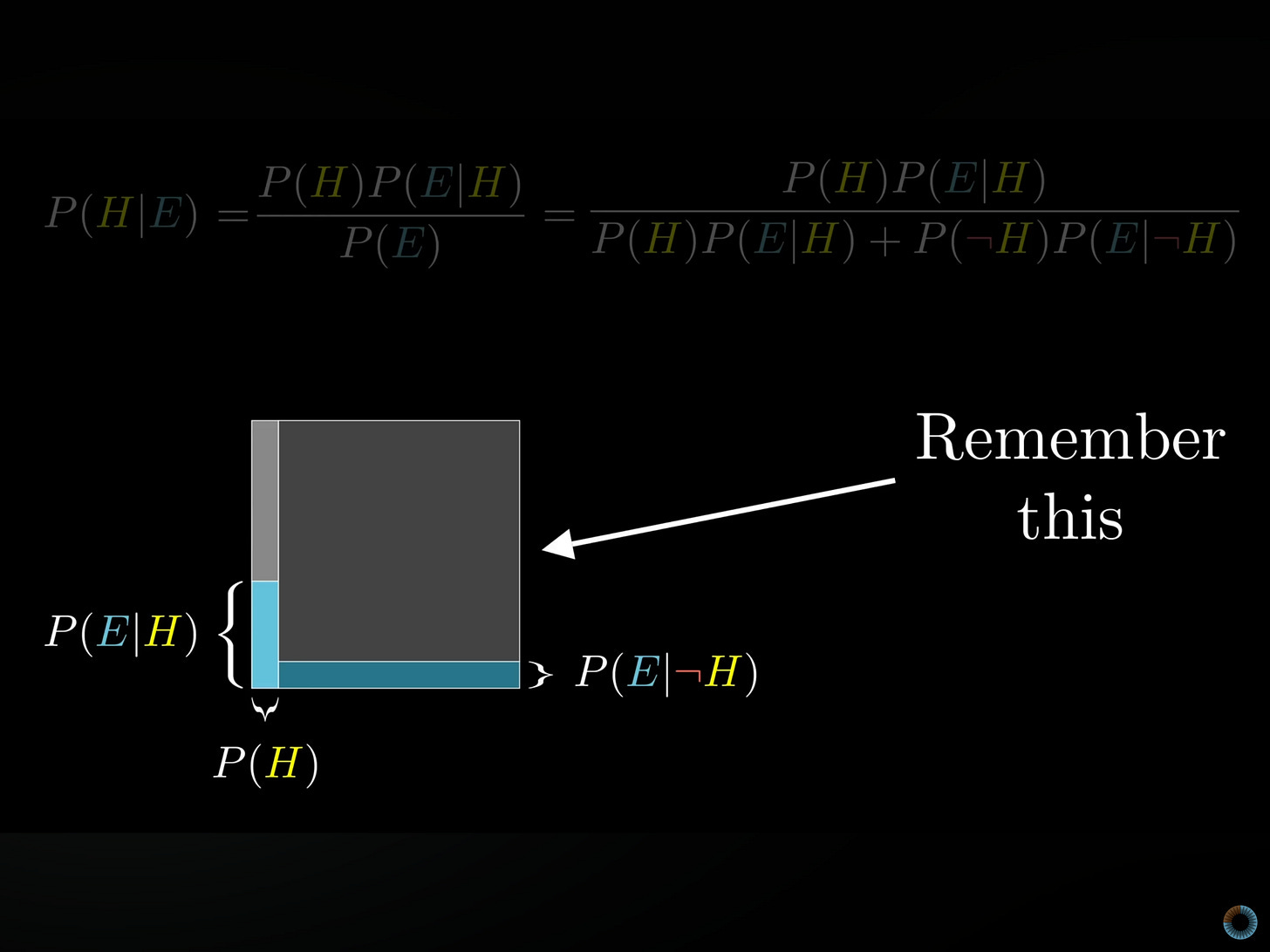
It probably won’t surprise you that I think part of the answer is Bayes’ theorem. But the equation is famously prickly and off-putting:

Over the years quite a few folks have attempted to explain it clearly. Eliezer wrote his famous essay back in 2003 (which Khalid Azad helpfully summarized in 2007), Scott’s written about it a number of times, Steven Pinker takes a whack at it in Rationality, Julia Galef speaks about it on BigThink, and so on and so forth. Recently, there’s even been a book explaining Bayes to babies. Bayesianism has become quite a racket!

I’ll be honest: I’ve learned something from each of these, but I think we can do even better. Specifically, I think that by using the paradigm I introduced in that book review — that of the recently-deceased philosopher Kieran Egan — we can make understanding and enjoying Bayes’ theorem a perfectly normal thing not just for quantitative geeks, but for more-or-less everyone. I’ve recently begun to test this out, and thought others might benefit from seeing what I’ve learned.

1: Ed philosophy on one foot

Your mind isn’t a general-purpose learning engine. Perhaps that sounds obvious to you, but among educators, I promise it’s not: I still hear teachers say that we know everyone can learn math on their own “because didn’t they learn language itself when they were babies?!”; I still hear people treat all learning as if it’s just facts on a forgetting curve.

Your mind, rather, is a Swiss Army knife — an assortment of oddball capacities kludged together over our long evolutionary history. In my book review, I showed how Kieran Egan found it useful to think of those tools being in five boxes:

And wow, that’s still way too complicated to easily grok. Two years later, can I do better? I think so.

Nowadays, I had to explain Egan while standing on one foot, I’d say something like this:

“We have old tools, and new tools. Join them together to help students fall in love with the world.”

There’s a lot wrong about that summary¹, but it’s at least a place to begin. The “new tools” are the ones created in the last couple thousand years, like careful concepts, finicky definitions, the scientific method, analysis & synthesis, and the quantification of everything. We here in the rationalist community love these things. Inculcating students in them is what much of the academic curriculum was built to do.

The “old tools”, meanwhile, are a motley bunch. Some have emerged through the tens of millennia of cultural evolution — stories, metaphors, rhyme & rhythm, jokes, and simple counting. Others are much, much older, coming out of our biological evolution — like our bodily senses, our capacity for mental imagery, gestures, mimicry, and personification.

These two toolsets create a chasm between how people today understand and live in the world. This is something that I suspect we all recognize: the old tools give us a way of understanding that’s embodied, narrative, and qualitative; the new ones give us one that’s abstracted, logical, and quantitative.

If this sounds like some sort of esoteric, speculative division, I’m doing a bad job explaining it. I mean to gesture at an idea that smart people have been pointing at for centuries. It’s at least similar to Nietzsche’s “Dionysian” vs. “Apollonian” modes, and to Claude Lévi-Strauss’s “the bricoleur” vs. “the engineer”, and to Alasdair MacIntyre’s critique of modernity. It’s near the heart of what Iain McGilchrist is describing in The Master and His Emissary. I think it’s the same thing as Erik Hoel’s “intrinsic” vs. “extrinsic” perspectives? It overlaps a lot with Kahneman’s “System 1” and “System 2” and with Jonathan Haidt’s “the elephant” and “the rider”. Heck, the lack of clarity on this divide is what makes Jordan Peterson’s dialogues with atheists so frustrating.

Anyhow, if we want to Eganize Bayes’ theorem, what we need to remember is that while the new tools have precision, the old tools have power. If we see Bayes’ theorem as one of the peaks of the new way of understanding, the question becomes, how can we use the old tools to secure Bayes in kids’ minds?

Anyhow, I’ve been working at this problem for a while. So far, I’ve come up with four ways to do it: make Bayes visual and intuitive, then make it vital, then make it obsolete.

2: Make it visual by turning equations into images

The boring ol’ way to explain Bayes, of course, is through an equation like the one above… and doing a Google image search for “Bayes’ theorem” overwhelmingly pulls up more examples of that than anything else.

It should go without saying that this isn’t the best way to teach this to the median middle schooler. Equations in general don’t come easily to most of us: recall that for the majority of our species’ existence, most people probably haven’t been able to count to ten. Worse, this equation doesn’t feature anything so simple as “a number” — instead it’s filled with wonky-looking variables with their own names and definitions that themselves need to be explained. For example:

P(B|A) is called the “likelihood”, and is the probability that the evidence is true, given that your hypothesis is true.

Blech. I’m not quite “innumerate” — once upon a time I scored an 800 on the quantitative section of my GRE — but when I typed in that definition a moment ago I literally felt my stomach lurch. If we want to pull normies in, we’ve gotta find some old tool that’s able to do some heavy lifting.

Images can do this. We shouldn’t be surprised: our pre-vertebrate ancestors evolved to see stuff, and to this day a substantial portion of our cortices is devoted to processing what our eyes take in. If we can find a way to represent this visually, we can sidestep this problem. And indeed on LessWrong, there’s an explanation that uses blobs, triangles, and pentagons; another person has built one out of Venn diagrams. My tastes, though, skew toward the simple, and I prefer the visualization created by the YouTuber 3Blue1Brown in a video that sets a new standard for elegance in explanation:

Let’s use a toy example to explain how this pretty picture works.

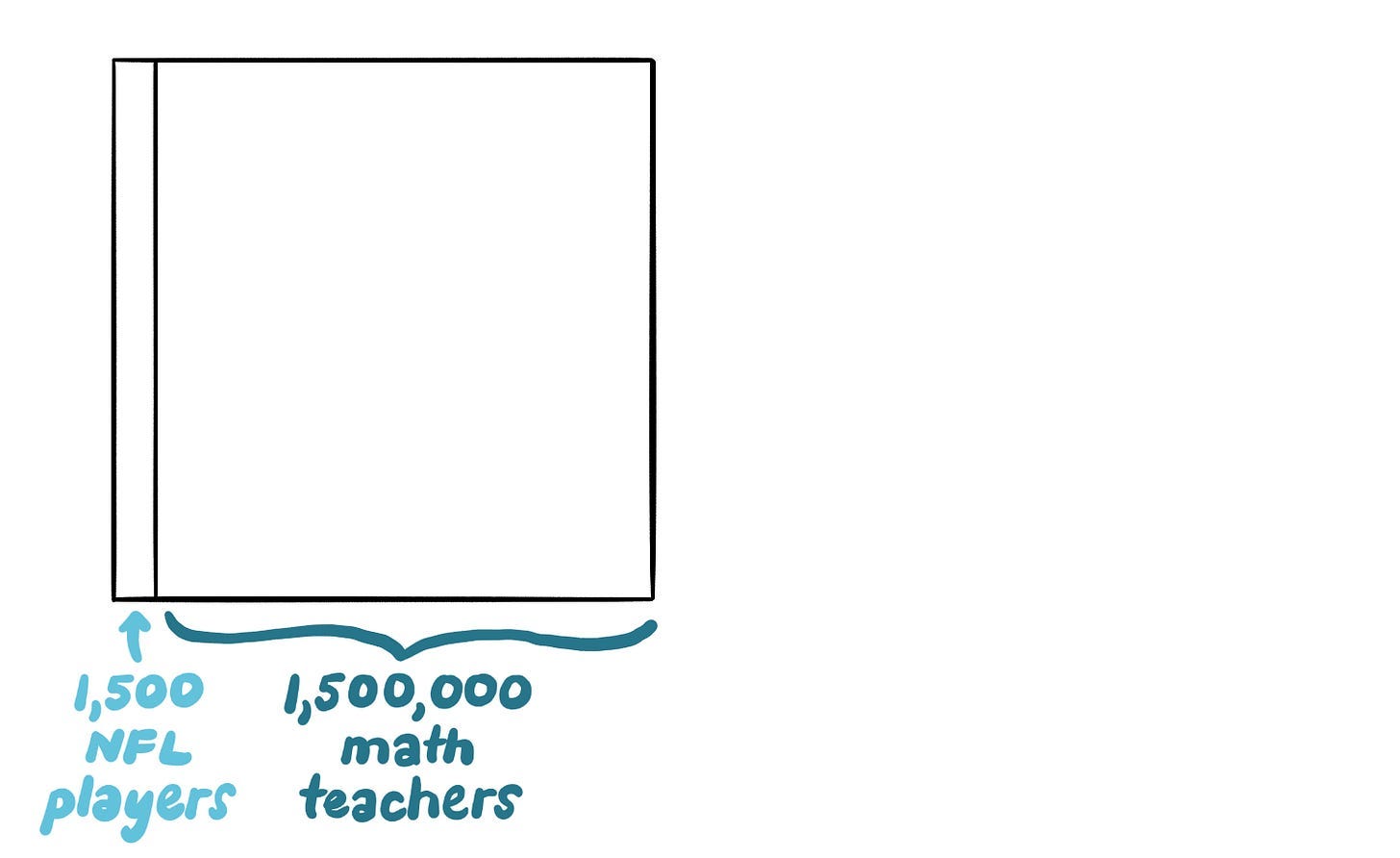
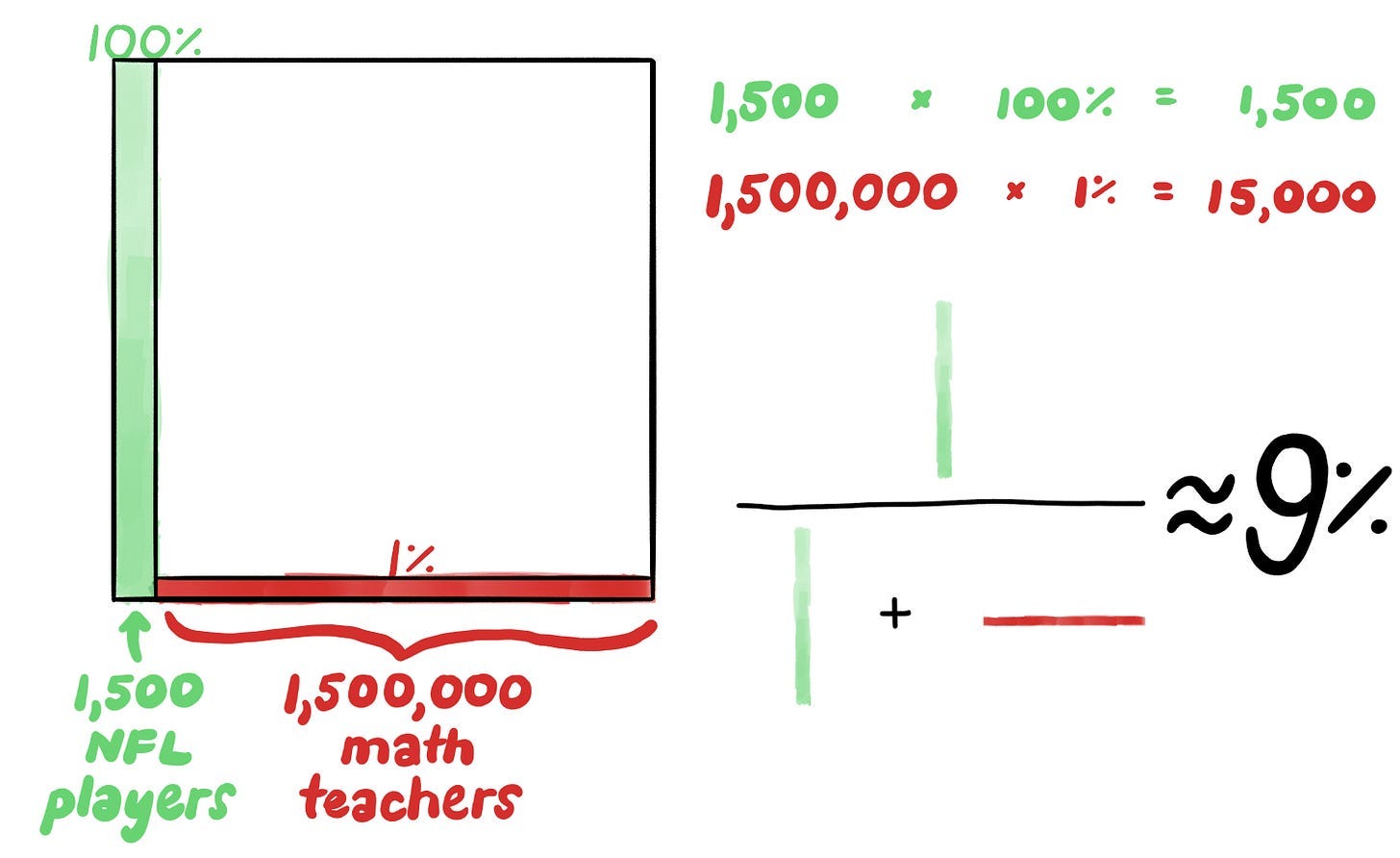
You’re lounging at the park, when you see a football being thrown out from a bush. The throw, you startle to see, is an utterly perfect spiral. Is the thrower a professional? Your dad’s a big football fan, and you suspect he’d be very impressed if you got an NFL player to autograph your face with the Sharpie marker you happen to have in your pocket. Alas, you’re too introverted to ask them, so you ask me to do it for you. I do, and I tell you that the person in the bush is either an NFL player or a math teacher. So what’s more likely — that an NFL player is hiding there, or a math teacher?

If you’re thinking carefully, you might note that some math teachers moonlight as football coaches: you guess that just 1% could throw a perfect spiral. If you’re thinking very carefully (or you’re just a trained Bayesian), you try to guess what the base rate is. How many NFL players are there in your area, and how many math teachers? A minute’s Googling tells you there your country has about 1,500 NFL players and 1,500,000 math teachers.

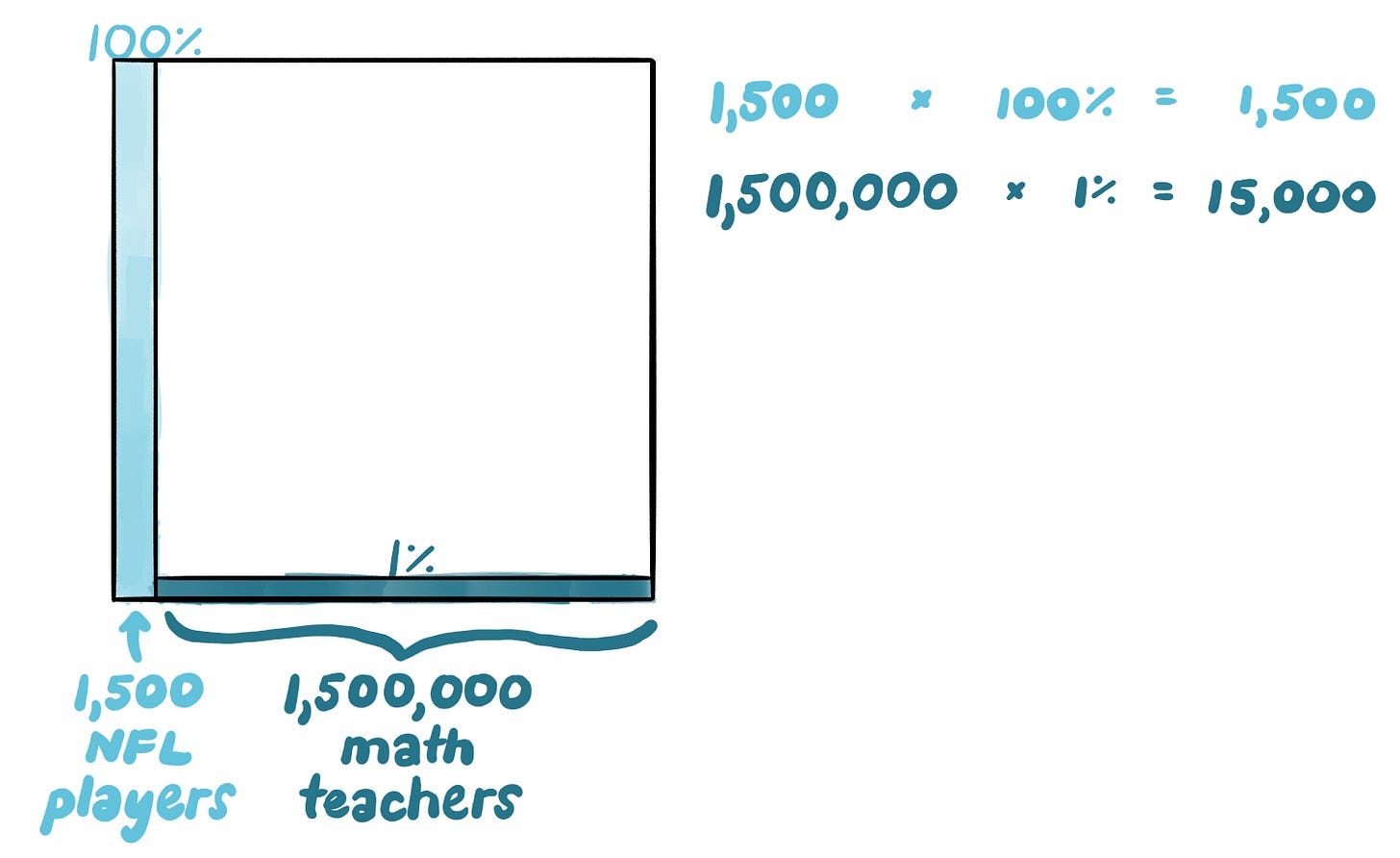
What are the odds it’s an NFL player? Draw a square. Sketch in the base (or prior) at the bottom — 1.5 thousand NFL players and 1.5 million math teachers.

Then sketch in the likelihoods: 100% and 1%.

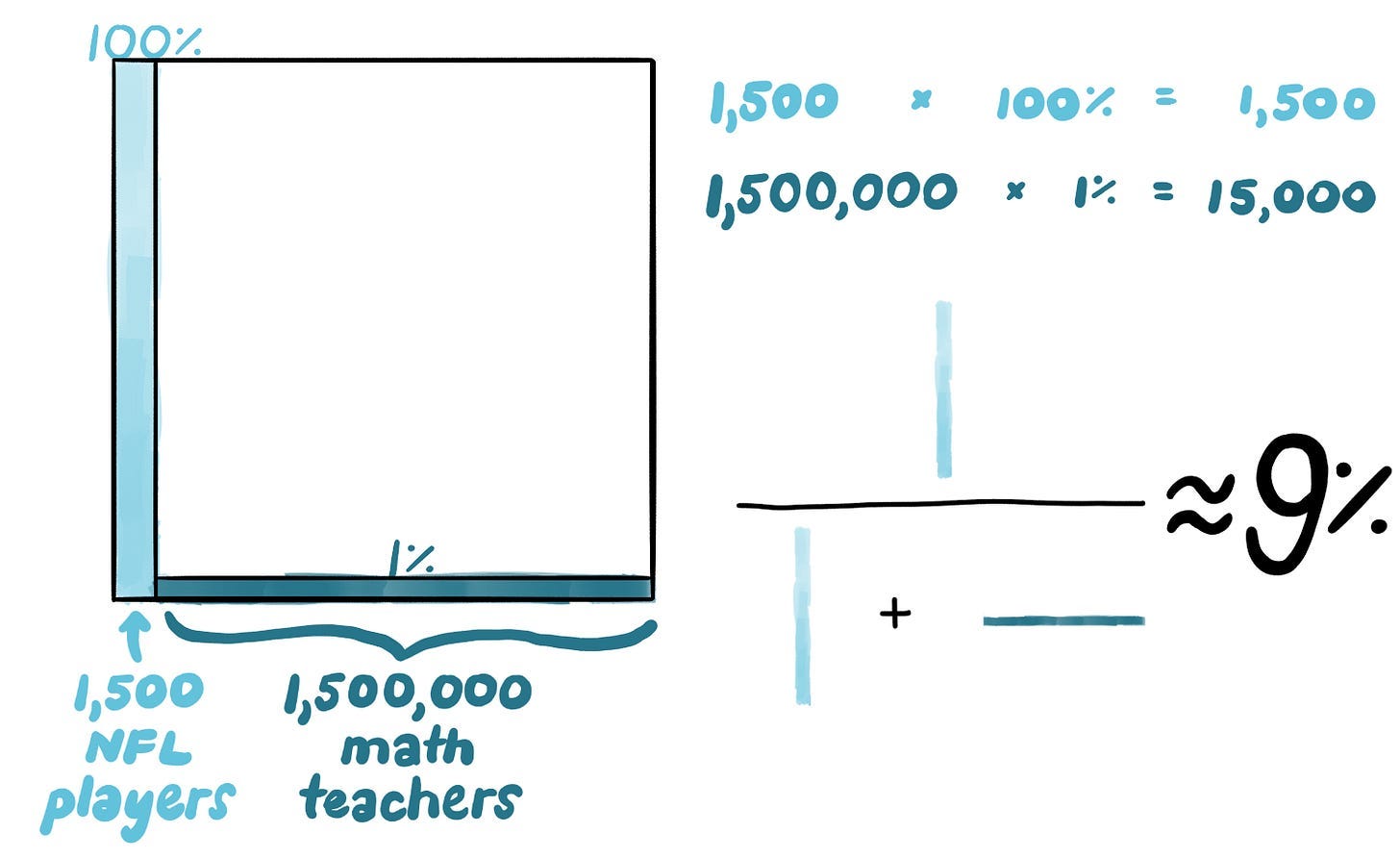
Then do the multiplication, and find that while there are indeed 1,500 NFL players in the country that could have thrown that ball, there are still far more math teachers — 15,000 — who could have thrown it!

If you’d like to find the new probability there’s an NFL player in that bush, just divide the shaded NFL players by all the shaded folks.

Imaginary Interlocutor: You’re suggesting we dumb Bayes’ theorem down, then?

Not at all — mathematically, they’re equivalent! In working through the problem visually, you do every single step that the equation does. There may be practical or aesthetic reasons someone might prefer working with the equation, but don’t forget what the purpose of the sword is.

3: Make it intuitive by tying abstractions to an emotional binary

Happily, this method seems to be taking off in our community. (See, for example, the second half of this Rational Animations video.²) But we can make it even more intuitive by drawing deeper from our evolutionary inheritance: before our ancestors could see, before they had cortices on which to represent the world around them, they had to answer an even simpler question: “is this place good or bad?” (Squint, and you’ll see the last three billion years of evolution as a series of attempts to answer that question with ever-greater precision.) This is the fundamental emotional binary. Value judgments, by necessity, seem to go all the way back to those crazy days when we were all archaebacteria.

This seems like one of those facts about the world that should be very important to philosophers, but how can we exploit this educationally? Simple: connect it to the abstractions of the Bayes box. Let’s be lazy, and call green “good” and red “bad”:

I.I.: What about people who are red-green colorblind?

Use whatever you’d like! Obviously, there’s nothing “good” about green, or “bad” about red. They’re cultural symbols — if you have a color pair that screams “good” and “bad” to you, use that instead. That said, if you’re using this to teach a class, you might want to lean into another emotional binary: empty/substantial. The first prior that we scribble down is usually going to be the one we’re hoping for (in this case, that it’s an NFL player). Make that more substantial by shading it as bolder. The second prior, make lighter:

So far, so good, but we haven’t left the realm of “teaching hacks”. I’ve found that this is one of the fail states when I introduce folks to Egan education — they mistake it for just another entry in the growing world of cog-sci-infused educational traditionalism.³

We care, of course, that Bayes is taught clearly to students — but we don’t want it to become for our students just another one of those “things I got an ‘A’ on and then never thought about again”. We want to infect students with the zeal of Bayesian thinking. We want it to upend the way they live in the world, and think about life, the universe, and everything. We want to make it matter to them.

This, I only recognized after writing that book review, is the unspoken assumption of Egan education. The matter with schooling is that too often, schooling doesn’t matter. The academic curriculum is filled with fossils — bizarre forms that once seem to have been alive and kicking but which now are just odd rocks. We want to make them come alive again. The promise of doing so is that when things emotionally matter to students, they will (by definition?) pay attention, work hard, and remember more.

So: how can we make Bayes matter to kids?

4: Make it vital by asking why people cared about it in the first place

Let’s look at the examples that the explanations use. The classic example (which is used by Eliezer, and which has a long history in conversations about Bayesianism) is mammograms — obviously, pretty far away from the concerns of most middle schoolers. The Bayes baby book does better, asking whether a random candy-less bite of a cookie is more likely to have been taken out of a cookie that has no candy pieces at all, or from one which has a few. Everyone loves candy, so this is sort of relevant [footnote: My two-year-old particularly loves this book, by the way, though she screams “BALL!” when she sees the colored candy pieces.], but it doesn’t exactly grab the emotions.

I.I.: Should we make the examples fun, then?

Eh. You’d think that as someone whose teaching style could be described as “wacky” and “manic” and “unhinged”, I’d be in favor of more silliness in schools. I suppose I am, but it’s important to note that “fun” by itself is unsubstantial. Education is a serious pursuit; souls are on the line.

I.I.: Then is it “relevancy” we need? (How could we make Bayesian reasoning relevant to middle schoolers’ everyday lives?)

Making what we teach relevant is essential — but be very careful about the assumptions packed into words like “relevant”, “useful”, and “practical”. When most of us hear those, we start thinking about the externals of our students’ lives. (How will this help them get a job? How will this help them become socially savvy?) Pause to consider how some of the most boring topics you learned in school were precisely those that were supposed to be “useful”. Here be dragons!

Consider, instead, just how irrelevant, useless, and impractical many of the things were that you threw yourself into when you were that age. Running a D&D campaign? Modding Half-Life? Learning Photoshop? Designing a fictional language? The real concerns of people run much deeper than what we’re likely to think of when we try to make something “relevant”.

Egan suggests a more helpful tact: look at where the skill came from. Who first created it?

I.I.: I’ve looked deeply into the life and times of the Reverend and Learned Thomas Bayes, Master of Arts, Fellow of the Royal Society, and I’ve come up with nothing.

Then look at who developed Bayesianism further. What community championed it? What sorts of things were driving them? Dear reader, we are that community! And why did we throw ourselves into Bayesian reasoning so fully? Certainly different people can give different answers, but my understanding is that many of us got interested in order to win online arguments against morons. My own start wasn’t particularly “relevant” to anything else I was doing: I got into Bayes to debate the historicity of Jesus. The people I see using it the most these days are mostly partisans (on both sides) of the God wars.

Presumably “does God exist?” is too spicy a vehicle for carrying Bayes into most schools, but that’s fine. We don’t need to emulate the specifics; we want to identify what more general psychological itches those fights were scratching. My read on this is that it’s about worldviews. In middle school, a lot of kids begin to wake up from the simplistic understandings of the universe they were told as a child: what’s really going on, and how can I show the world that those fools who disagree with me are wrong?

Randall Munroe, https://xkcd.com/386/

A lot of the kids who I work with (not a representative sample: they skew toward the gifted and hyperactive sides of the spectrums) are fascinated by cryptids, UFOs, and psychic phenomena. So for them, I’ve been crafting courses that teach Bayes as a way to get clear on that stuff.

I.I.: That’s pseudoscientific schlock — you can’t teach that in school!

You can’t teach it, but you can explore it. (And it’ll elicit far fewer emails to the principal than evaluating the existence of God.)

I.I.: What I meant to say was please don’t teach pseudoscientific schlock in schools. Instead, use Bayes to teach what’s actually important.

Please don’t refuse to take children seriously. My probability for Bigfoot is way under 1%, but when we assume an answer to (for example) whether Bigfoot is real and simply repeat it to kids, we deny them an opportunity ripe for sharpening their intellects.

I.I.: But cryptids are so low-brow…

A sign of how deeply appealing they are for multitudes of people! Things like this are a road to intellectualism for the masses; we ignore it to the detriment of some of the kids who need it most. Even the cretin who bullied me in sixth grade was, in his spare time, trying to understand the world. Heck, we’re all naturally drawn to understanding the edges of things. Where does fact end and fiction begin? There’s a reason the History Channel inevitably morphed into the “ancient aliens” channel.

Taking this seriously is how I came up with a set of online summer camps. The weeklong course last year used Bigfoot to get kids to experience using Bayes theorem. The one from this summer will deepen that by looking at claims of sea monsters. Year 3’s will extend this, asking when we should trust the media on UFOs UAPs. Year 4’s will hold a bright light up to academic, peer-reviewed sources by looking closely into the evidence for psychic powers, and year 5’s will try to suss out the edges of science itself by looking into the evidence for ghosts. Whatever else these summer camps accomplish, I hope they’ll prepare my students for whatever dubious assertions they run across on YouTube.

5: Repeat it until it’s obsolete

I’ve spread my classes across multiple summers not (merely) because I’m lazy, but because it’s useful to keep working on the theorem across multiple years. Because we can’t ignore the fact that “computing the Bayesian probabilities” isn’t actually a silver bullet to rationality. Most of us know people who’ve earnestly used Bayes to “prove” things that are straight-up insane. As my science advisor warned me when I was deciding whether to make these courses:

Bayesian reasoning can become confirmation bias on steroids. You have to be humble in your analysis, because there are SO MANY DIFFERENT WAYS IT CAN GO WRONG.

There really are so, so many ways it can go wrong. And the kids need to make each and every one of them.

I.I.: Because repetition builds mastery, right?

Yes, but then we want to build past mastery. “Mastery” has become something of a buzzword lately, but something that’s been forgotten in our love of deliberate practice is that the journey to becoming educated is harder and longer than just mastering a set of skills. It requires being able to stick your head out of the Matrix and ask, “wait, how useful is this stuff, actually?” We want to help kids get so good with drawing Bayes boxes that they realize they’ll never be perfect at it… and that their best hope for becoming rational is to reason together with people they disagree with.

I.I.: Is it even useful to teach middle schoolers to literally crunch these numbers? Shouldn’t we teach “scout mindset” first?

Indeed, this is the question — scouting first, or Bayes Boxes?

I used to think that formally learning Bayes’ theorem was difficult and better saved to the end of learning rationality. Now I see things differently — though not because I think we should expect kids to sit down and do the math on their own, in their everyday lives. (Do any of us actually do that?⁴) I think once we make it easy — and the math really is easy, once you explain it visually and do it a couple times — then we should teach Bayes first, because…

Bayes is a great excuse to think with other people.

Drawing little rectangles is a great way to see where you disagree with somebody. You think aliens have infiltrated the world’s governments? Cool! Let’s talk priors, and see where we draw our vertical lines. You think you saw a ghost, and now it’s rocked your worldview? Let’s talk about how strongly we should update from personal experience. Get a napkin — let’s draw some cute boxes.

This, I think, is actually the deepest value of teaching kids Bayes: it’s a way to get them to converse with people whose views they think are stupid. And it’s only through actually doing that that we have any chance of helping people become rational. Such conversations (done with checking each other’s math) are the way to inculcate an openness to being wrong, a detached self-worth, comfort with uncertainty, and all the other aspects of what Julia Galef has so winsomely dubbed scout mindset. Approached this way, Bayes isn’t the weirdo, quant-y capstone to scout mindset — it’s the publicly-accessible front door.

6: Where are we, now?

I.I.: You claim to be promoting something new, but it seems to me like you’re just describing the rationalist community.

Indeed I am! My claim wasn’t that this method of explaining Bayes goes beyond what’s practiced in the community — just that it’s likely to do a better job pulling kids into the sorts of intense, curiosity-fueled relationships that our community excels at.

And I think this is something worth working hard to achieve. According to the historian Reviel Netz, creating a stable culture like this was the One Weird Trick behind the “Greek Miracle” around 500 BCE. When this culture finally fizzled out, society reverted to valuing authority and uniformity. In the account of the historian and philosopher Michael Strevens, the Scientific Revolution was launched when thinkers found a new social practice that could gin up these cultural norms again. My hope is that by helping kids do Bayes’ theorem together — and starting with questions they’re actually excited about — can spark something similar in schools now.

At the end of my book review, I floated my thought that the best way to express Egan’s paradigm is to say it “re-humanizes academics”. That’s what I’ve tried to do here: to take an important component of modern thinking, make it easy to learn by using tools from our evolutionary past, and make it vital to kids. And all of this is toward the goal of helping lift them out of the Matrix, so they can see what they’re studying as imperfect, historically-contingent tools that they can, as autonomous agents, choose to use as they see fit.

If that much human richness and potential can be pulled out of just one piece of the curriculum (albeit an important bit!), what could be achieved if we re-humanize the rest? What hidden vitality lies in poetry, or geography, or punctuation? With ancient history, or economics, or biology? Maybe education isn’t a lost cause after all.

In any case, if you have a notion about how to further unveil the glories of Bayes’ theorem to kids, I’m eager for your take.

1. Where’s the sense that story undergirds everything? Where’s the recognition that these types of tools create qualitatively different ways of understanding that war against one another? Where’s the beauty, the existential wrangling, the bewilderment…?

2. And I think I heard Aella mention it on a podcast?

3. Not that I’m opposed to cog-sci-infused educational traditionalism! For anyone looking for such, I recommend Zach Groshell’s Just Tell Them: The Power of Explanations and Explicit Teaching.

4. I meant that rhetorically, but now I’m actually really interested.